Гауссовские процессы

Миша

Когда я начинал изучать МЛ у меня в голове всё не могли уложиться гауссовские процессы: что там за матрица, что за ядерная функция? Давайте попробую разложить по полочкам.

Для начала представляем себе многомерную гауссиану. Если она будет «круглая», то параметры точки, засэмплированной из этого нормального распределения не будут зависеть друг от друга. Если же гауссиана «вытянутая» вдоль нескольких осей — наоборот. То есть если вы зафиксируете какое-то измерение вектора и скажете, что он взят из этого распределения — остальные измерения должны будут подстроиться под него (смотрите на гифку).

Пояснение: зафиксировать измерение = сделать срез нормального распределения.

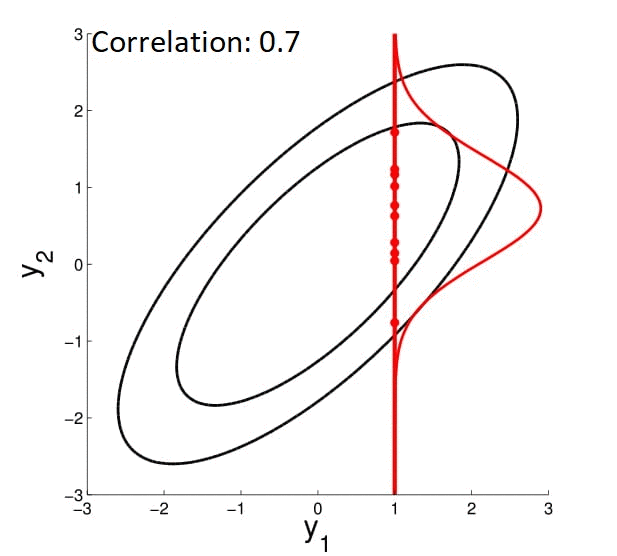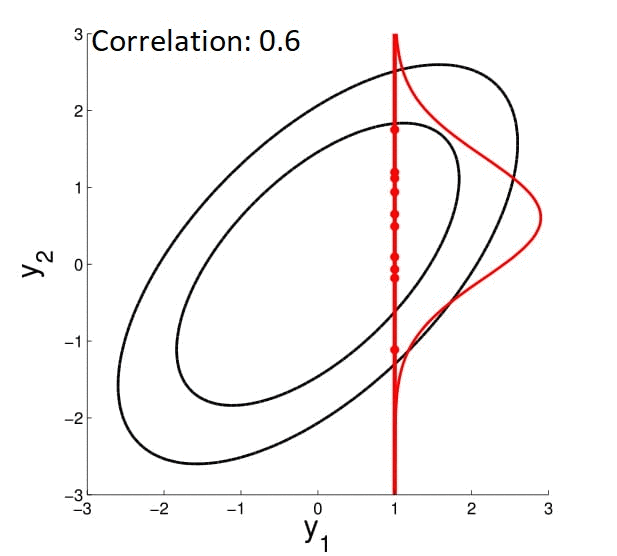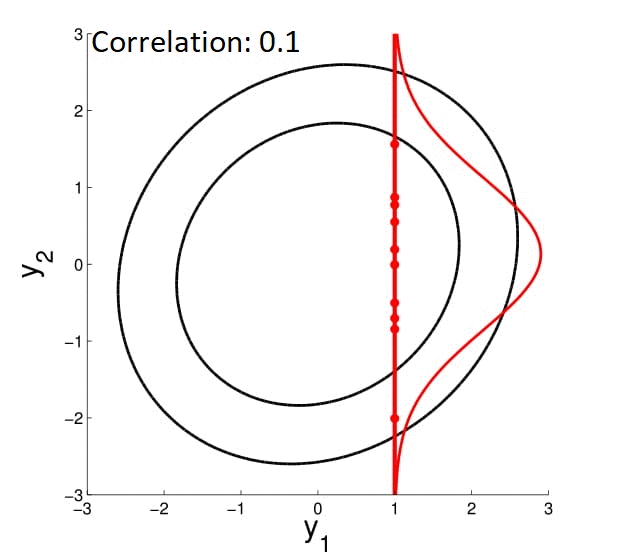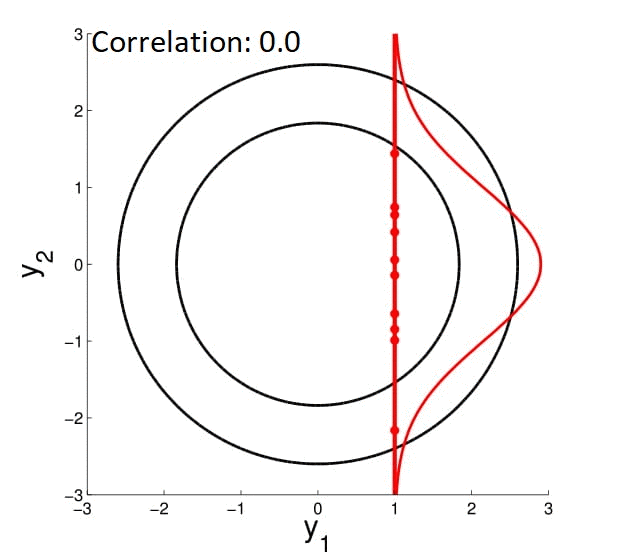
Выбрав какое-то измерение и зафиксировав его, мы накладываем ограничения на остальные, но зачем это нам? Сейчас дойдём. Для этого давайте посмотрим на какие измерения накладываются ограничения. Как это понять? Мы уже заметили, что у круглой гауссианы измерения не взаимозависимы, а у вытянутой — наоборот. Получается, что за это должен отвечать какой-то из параметров нормального распределения. Очевидно, что не среднее, значит матрица ковариации. Посмотрим на неё: у «круглой» гауссианы она будет иметь ненулевые элементы только на диагонали, а у «вытянутой» будут уменьшаться от диагонали к правому верхнему и левому нижнему углам.

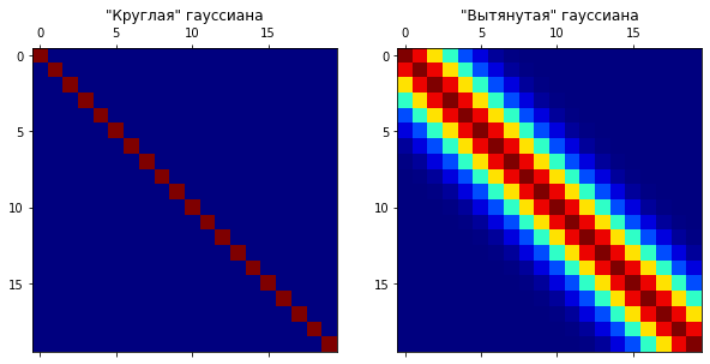
Что это значит? Это значит, что первое измерение будет сильно влиять на второе, но почти никак на 20-е, оно будет иметь большую ковариацию со вторым. То есть, по сути, с помощью такой матрицы мы задаём то, как одни измерения влияют на другие.

Давайте посмотрим на гифку: на ней изображены случайно взятые точки из 20-мерной вытянутой гауссианы. По горизонтали индексы измерений, а по вертикали значения. По сути это такой странный способ нарисовать многомерную точку.

Пояснение: один график — одна случайная точка, взятая из нашей гауссианы.

Видим забавную вещь: координаты точки как-то подозрительно плавно изменяются, соседние измерения похожи друг на друга. Это происходит потому, что матрица ковариации задаёт ограничения на соседей (левый нижний угол гифки выше, значения матрицы изменяются от синего к красному, как от меньшего к большему).

Что же случится, если мы зафиксируем одну из точек? Она будет влиять на соседей: задавать распределения на них! Более вероятными окажутся значения, похожие на зафиксированную точку и менее — далёкие от неё.

Смотрим на гифку ниже и вдохновляемся: первое измерение зафиксировано, остальные подстраиваются под него, всё круто (причём первое измерение влияет на второе сильно, 0.9, а на пятое слабо, 0.4). По сути мы придумали способ, который позволяет зафиксировав некоторое кол-во точек узнать что-то о распределениях других.

Но. Можно справедливо заметить, что такой способ будет работать только для заранее заданного количества измерений, в чём вообще смысл придумывать что-то настолько сложное, что даже не может работать с непрерывными точками? На самом деле может. Именно на этом моменте случается разрыв шаблона и именно эту фигню я не смог сразу понять когда-то давно, когда начинал учить МЛ. Мы переходим от дискретной матрицы ковариации к непрерывной. Как к непрерывной, что значит к непрерывной? Сейчас разберёмся.
Представим, что наша матрица ковариации задана как K(i, j) , где i и j это индекс столбца и строки (измерения i и измерения j, то как первое из них влияет на второе), а K — какая-то функция от них (ядерная функция это именно она, кстати).

Пояснение: каждая ячейка матрицы получается подстановкой индекса строки и столбца в K.

Почему бы не попробовать вставлять в K(∙, ∙) вместо индексов измерений произвольные числа из ℝ? Почему бы и нет, оказывается, что наша дискретная матрица превралась в непрерывную, теперь как бы «существуют» измерения с индексами 2.5, π или √3, а не только классические 1, 2, 3, … И, оказывается, мы можем точно так же задавая некоторые координаты, ограничивать рядом лежащие измерения, неважно целые ли у них индексы.

Всё это звучит очень сложно и непонятно, пока ты не смотришь на картинку ниже. На ней показаны:

Непрерывная «матрица ковариации» (слева внизу), полученная с помощью K (большие значения — красным, маленькие — синим).
Распределения для неизвестных точек (синим), при заданных измерениях — красных точках (на графике x-y).

Здесь нам известны какие-то данные — красные точки. Благодаря им мы знаем не только где наиболее вероятно располагаются другие точки (тёмно-синяя линия), но и распределения на них. Выбирая различные K, мы можем получать различные распределения на неизвестные нам данные.

И, по сути, всё.

Резюмируем:

Есть функция K , принимающая два числа, с помощью неё мы можем выяснять как распределены неизвестные нам данные, опираясь на известные. K задаёт вид матрицы ковариации и именно от выбора K распределения будут выглядеть тем или иным образом. Подробнее про выборK можно почитать, например, тут: kernel cookbook.

Подробнее писать уже не буду, а то и так уже много вышло. Для желающих ознакомиться ещё подробнее советую вот этот шикарный блогпост.